CNN에서 64x64x3의 크기의 입력을 받는다.(컬러 채널 3개를 가진 ‘channel_last’ 포맷, NHWC)
입력 데이터는 4개의 층을 지나 32개, 64개, 128개, 256개의 특성 맵을 만든다.
(3x3크기의 커널을 가진 필터를 사용, 2x2 크기의 폴리을 사용, 두개의 드롭아웃 층)
model=tf.keras.Sequential([
tf.keras.layers.Conv2D(32, (3, 3), padding='same', activation='relu'),
tf.keras.layers.MaxPooling2D((2, 2)),
tf.keras.layers.Dropout(rate=0.5),
tf.keras.layers.Conv2D(64, (3, 3), padding='same', activation='relu'),
tf.keras.layers.MaxPooling2D((2, 2)),
tf.keras.layers.Dropout(rate=0.5),
tf.keras.layers.Conv2D(128, (3, 3), padding='same', activation='relu'),
tf.keras.layers.MaxPooling2D((2, 2)),
tf.keras.layers.Conv2D(256, (3, 3), padding='same', activation='relu')])
model.compute_output_shape(input_shape=(None, 64, 64, 3))
TensorShape([None, 8, 8, 256])
위의 모델을 64x64x3 데이터가 통과하게 되면, 8x8x256 데이터가 출력된다.
이를 Flatten 하게 되면, 16,384가 된다.
전역 평균 풀링(global average-pooling)전역 평균 풀링층을 추가한다. 이 층은 각 특성 맵의 평균을 독립적으로 계산하기 때문에
은닉 유닛이 256개로 줄어든다.
[배치크기 x 64 x 64 x 8] 크기의 특성 맵에서 전역 평균 풀링은 각 채널의 평균을 계산하기 때문에
출력은 [배치크기 x 8]이 된다
위의 [None x 8 x 8 x 256]은 [None x 256]이 된다.
전역평균풀링 추가
model.add(tf.keras.layers.GlobalAveragePooling2D())
model.compute_output_shape(input_shape=(None, 64, 64, 3))
완전 연결(밀집)층 추가 & build완전연결층의 활성화 함수가 sigmoid가 되면 확률을
None이 되면 로짓 값을 출력한다.
model.add(tf.keras.layers.Dense(1, activation=None))
tf.random.set_seed(1)
model.build(input_shape=(None, 64, 64, 3))
model.summary()
Model: "sequential_2"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
conv2d_12 (Conv2D) (None, 64, 64, 32) 896
_________________________________________________________________
max_pooling2d_9 (MaxPooling2 (None, 32, 32, 32) 0
_________________________________________________________________
dropout_3 (Dropout) (None, 32, 32, 32) 0
_________________________________________________________________
conv2d_13 (Conv2D) (None, 32, 32, 64) 18496
_________________________________________________________________
max_pooling2d_10 (MaxPooling (None, 16, 16, 64) 0
_________________________________________________________________
dropout_4 (Dropout) (None, 16, 16, 64) 0
_________________________________________________________________
conv2d_14 (Conv2D) (None, 16, 16, 128) 73856
_________________________________________________________________
max_pooling2d_11 (MaxPooling (None, 8, 8, 128) 0
_________________________________________________________________
conv2d_15 (Conv2D) (None, 8, 8, 256) 295168
_________________________________________________________________
global_average_pooling2d (Gl (None, 256) 0
_________________________________________________________________
dense (Dense) (None, 1) 257
=================================================================
Total params: 388,673
Trainable params: 388,673
Non-trainable params: 0
_________________________________________________________________
CNN에서 파라미터의 개수는
(3x3x(이전채널수)+1)x채널수
ex) conv2d_15의 파라미터 수:
(3x3x128+1)x256=295,168
compile & fit(with Giovanni)하나의 출력 유닛을 가진 이진분류(MALE, FEMALE)이므로 BinaryCrossentropy를 사용한다.
마지막 층에 activation=None으로 지정했기 때문에(시그노이드 비활성화)모델의 출력은 로짓이다.
BinaryCrossentropy 클래스에서 from_logits=True로 지정하면, 손실함수가 내부적으로 시그모이드 함수를 적용한다.
모델의 마지막층을 시그모이드로 하는 것 보다 더 효과적인 방법이다.
model.compile(optimizer=tf.keras.optimizers.Adam(), loss=tf.keras.losses.BinaryCrossentropy(from_logits=True), metrics=['accuracy'])
history=model.fit(ds_train, validation_data=ds_valid, epochs=20, steps_per_epoch=steps_per_epoch)
500/500 [==============================] - 10s 10ms/step - loss: 0.6386 - accuracy: 0.6132 - val_loss: 0.5342 - val_accuracy: 0.6790
Epoch 2/20
500/500 [==============================] - 5s 10ms/step - loss: 0.5421 - accuracy: 0.7042 - val_loss: 0.4711 - val_accuracy: 0.7270
Epoch 3/20
500/500 [==============================] - 5s 10ms/step - loss: 0.4826 - accuracy: 0.7524 - val_loss: 0.4330 - val_accuracy: 0.7640
Epoch 4/20
500/500 [==============================] - 5s 10ms/step - loss: 0.4183 - accuracy: 0.7964 - val_loss: 0.3262 - val_accuracy: 0.8260
Epoch 5/20
500/500 [==============================] - 5s 11ms/step - loss: 0.3591 - accuracy: 0.8262 - val_loss: 0.3030 - val_accuracy: 0.8110
Epoch 6/20
500/500 [==============================] - 5s 11ms/step - loss: 0.3046 - accuracy: 0.8593 - val_loss: 0.3333 - val_accuracy: 0.7970
Epoch 7/20
500/500 [==============================] - 5s 10ms/step - loss: 0.2755 - accuracy: 0.8744 - val_loss: 0.2373 - val_accuracy: 0.8620
Epoch 8/20
500/500 [==============================] - 5s 10ms/step - loss: 0.2561 - accuracy: 0.8861 - val_loss: 0.1832 - val_accuracy: 0.9160
Epoch 9/20
500/500 [==============================] - 5s 10ms/step - loss: 0.2408 - accuracy: 0.8926 - val_loss: 0.2563 - val_accuracy: 0.8620
Epoch 10/20
500/500 [==============================] - 5s 10ms/step - loss: 0.2246 - accuracy: 0.9018 - val_loss: 0.2578 - val_accuracy: 0.8550
Epoch 11/20
500/500 [==============================] - 5s 10ms/step - loss: 0.2155 - accuracy: 0.9042 - val_loss: 0.2194 - val_accuracy: 0.8680
Epoch 12/20
500/500 [==============================] - 5s 10ms/step - loss: 0.2075 - accuracy: 0.9107 - val_loss: 0.1812 - val_accuracy: 0.9070
Epoch 13/20
500/500 [==============================] - 5s 10ms/step - loss: 0.1962 - accuracy: 0.9147 - val_loss: 0.2364 - val_accuracy: 0.8630
Epoch 14/20
500/500 [==============================] - 5s 10ms/step - loss: 0.1939 - accuracy: 0.9151 - val_loss: 0.1490 - val_accuracy: 0.9350
Epoch 15/20
500/500 [==============================] - 5s 10ms/step - loss: 0.1852 - accuracy: 0.9199 - val_loss: 0.1824 - val_accuracy: 0.8970
Epoch 16/20
500/500 [==============================] - 5s 10ms/step - loss: 0.1827 - accuracy: 0.9206 - val_loss: 0.1763 - val_accuracy: 0.8940
Epoch 17/20
500/500 [==============================] - 5s 10ms/step - loss: 0.1715 - accuracy: 0.9279 - val_loss: 0.1780 - val_accuracy: 0.9070
Epoch 18/20
500/500 [==============================] - 5s 10ms/step - loss: 0.1685 - accuracy: 0.9261 - val_loss: 0.1829 - val_accuracy: 0.9020
Epoch 19/20
500/500 [==============================] - 5s 10ms/step - loss: 0.1653 - accuracy: 0.9299 - val_loss: 0.1629 - val_accuracy: 0.9200
Epoch 20/20
500/500 [==============================] - 5s 10ms/step - loss: 0.1596 - accuracy: 0.9324 - val_loss: 0.1558 - val_accuracy: 0.9190
Graph
import matplotlib.pyplot as plt
hist=history.history
x_arr=np.arange(len(hist['loss']))+1
fig=plt.figure(figsize=(12, 4))
ax=fig.add_subplot(1, 2, 1)
ax.plot(x_arr, hist['loss'], '-o', label='Train loss')
ax.plot(x_arr, hist['val_loss'], '--<', label='Validation loss')
ax.legend(fontsize=15)
ax.set_xlabel('Epoch', size=15)
ax.set_ylabel('Loss', size=15)
ax=fig.add_subplot(1, 2, 2)
ax.plot(x_arr, hist['accuracy'], '-o', label='Train acc.')
ax.plot(x_arr, hist['val_accuracy'], '--<', label='Validation acc.')
ax.legend(fontsize=15)
ax.set_xlabel('Epoch', size=15)
ax.set_ylabel('Accuracy', size=15)
plt.show()
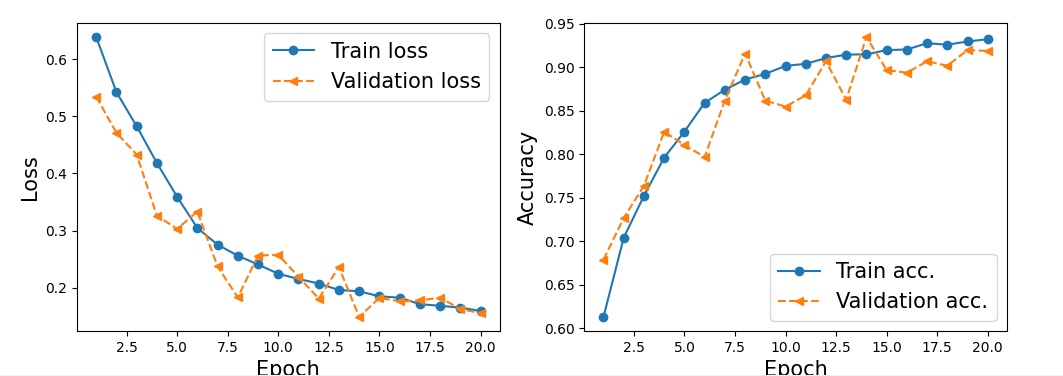
검증 손실이 평탄한 영역으로 수렴하지 않았다.
추가적인 에포크 훈련이 더 필요할 경우 fit를 통해 이어서 훈련이 가능하다.
10 epochs training 이어서 하기
history=model.fit(ds_train, validation_data=ds_valid, epochs=30, initial_epoch=20, steps_per_epoch=steps_per_epoch)
Epoch 21/30
500/500 [==============================] - 5s 10ms/step - loss: 0.1588 - accuracy: 0.9309 - val_loss: 0.1249 - val_accuracy: 0.9410
Epoch 22/30
500/500 [==============================] - 5s 10ms/step - loss: 0.1524 - accuracy: 0.9356 - val_loss: 0.1445 - val_accuracy: 0.9230
Epoch 23/30
500/500 [==============================] - 5s 10ms/step - loss: 0.1449 - accuracy: 0.9400 - val_loss: 0.1344 - val_accuracy: 0.9400
Epoch 24/30
500/500 [==============================] - 5s 10ms/step - loss: 0.1409 - accuracy: 0.9406 - val_loss: 0.1249 - val_accuracy: 0.9420
Epoch 25/30
500/500 [==============================] - 5s 10ms/step - loss: 0.1391 - accuracy: 0.9419 - val_loss: 0.1308 - val_accuracy: 0.9380
Epoch 26/30
500/500 [==============================] - 5s 10ms/step - loss: 0.1294 - accuracy: 0.9467 - val_loss: 0.1427 - val_accuracy: 0.9290
Epoch 27/30
500/500 [==============================] - 5s 10ms/step - loss: 0.1355 - accuracy: 0.9441 - val_loss: 0.1257 - val_accuracy: 0.9490
Epoch 28/30
500/500 [==============================] - 5s 10ms/step - loss: 0.1271 - accuracy: 0.9474 - val_loss: 0.1180 - val_accuracy: 0.9430
Epoch 29/30
500/500 [==============================] - 5s 10ms/step - loss: 0.1218 - accuracy: 0.9484 - val_loss: 0.1389 - val_accuracy: 0.9340
Epoch 30/30
500/500 [==============================] - 5s 10ms/step - loss: 0.1242 - accuracy: 0.9496 - val_loss: 0.1489 - val_accuracy: 0.9270
evaluate with test data(Celeb_a dataset(self making) 참조)
test_results=model.evaluate(ds_test)
print('테스트 정확도: {:.2f}%'.format(test_results[1]*100))
테스트 정확도: 87.50%
model predict로짓으로 값이 출력되기 떄문에 tf.sigmoid 함수를 사용해서 클래스 1의 확률을 얻을 수 있다.
(다중 분류일 경우 tf.math.softmax)
ds=ds_test.unbatch().take(10)
pred_logits=model.predict(ds.batch(10))
probas=tf.sigmoid(pred_logits)
probas=probas.numpy().flatten()*100
probas=probas.numpy
fig=plt.figure(figsize=(15, 7))
for j, example in enumerate(ds):
ax=fig.add_subplot(2, 5, j+1)
ax.set_xticks([]);ax.set_yticks([])
ax.imshow(example[0])
if example[1].numpy()==1:
label='M'
else:
label='F'
ax.text(0.5, -0.15, 'GT: {:s}\nPr(Male)={:.0f}%'.format(label, probas[j]), size=15, horizontalalignment='center', verticalalignment='center', transform=ax.transAxes)
plt.tight_layout()
plt.show()

